The last two weeks have been quite hectic and challenging. I spent most of these two weeks working on the Farneback algorithm. Using 1D correlations for polynomial expansion turned out quite difficult to understand and thus I had to put in a lot of extra hours cutting time from the Haar-like features so as to avoid falling behind on my timeline. But the disaster seems to be successfully averted.
Farneback Dense Optical Flow
This is a method for dense optical flow estimation developed by Gunnar Farneback and described in his paper Two-Frame Motion Estimation Based on Polynomial Expansion. It computes the optical flow for all the points in the frame using the polynomial representation of the images. The idea of polynomial expansion is to approximate the neighbourhood of a point in a 2D function with a polynomial as described here in the author's thesis. Displacement fields are estimated from the polynomial coefficients depending on how the polynomial transforms under translation.
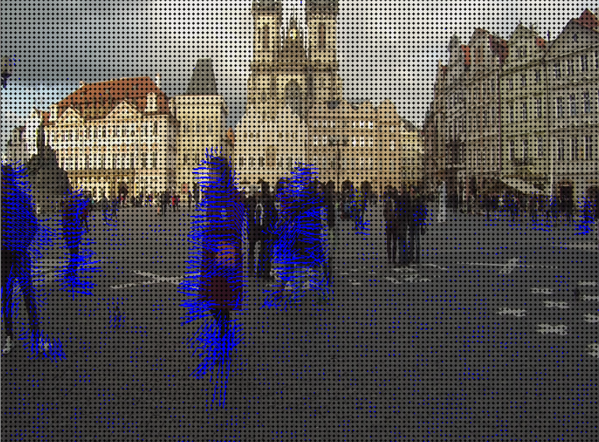Dense optical flow found for a street scene.
I spent most of the third week trying to implement the polynomial expansion part of the algorithm. The naive implementation which uses simple matrix multiplication was very simple to implement but using 1D correlations of the applicability and basis functions was quite difficult to understand and this proved to be a major roadblock in the process of implementing this algorithm. I spoke to my mentor regarding this and decided to put this algo on hold and work on the Haar-like features. After finishing up with Haar I picked this algo again and finally got to completely understanding it. I finished up a rough first attempt and sent the PR #3.
Haar-like Features
Haar-like features are digital image features used in object recognition. They owe their name to their intuitive similarity with Haar wavelets and were used in the first real-time face detector developed by Viola and Jones. Original work on the Haar-like features is found in this paper by Oren, Papageorgiou, Sinha, Osuna and Poggio.
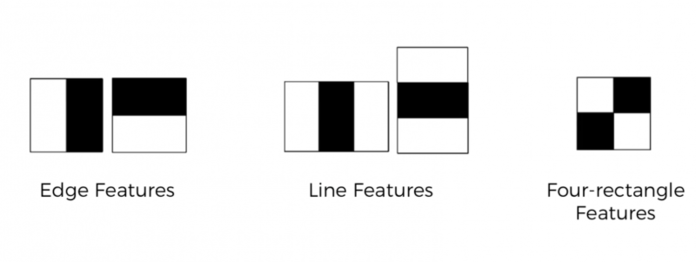Different rectangular Haar-like features.
A simple rectangular Haar-like feature can be defined as the difference of the sum of pixels of areas inside the rectangle, which can be at any position and scale within the original image. This modified feature set is called 2-rectangle feature. Viola and Jones also defined 3-rectangle features and 4-rectangle features. The values indicate certain characteristics of a particular area of the image. Each feature type can indicate the existence (or absence) of certain characteristics in the image, such as edges or changes in texture. For example, a 2-rectangle feature can indicate where the border lies between a dark region and a light region.
One of the contributions of Viola and Jones was to use summed-area tables, which they called integral images. Integral images can be defined as two-dimensional lookup tables in the form of a matrix with the same size of the original image. Each element of the integral image contains the sum of all pixels located on the up-left region of the original image (in relation to the element's position). This allows to compute sum of rectangular areas in the image, at any position or scale, using only four lookups. Each Haar-like feature may need more than four lookups, depending on how it was defined. Viola and Jones's 2-rectangle features need six lookups, 3-rectangle features need eight lookups, and 4-rectangle features need nine lookups.
I implemented this algorithm in between the Farneback one. The code makes use of the integral_image() function and the boxdiff() function from Images.jl package to calculate the features efficiently. Two functions are provided: one for finding the coordinates of all the Haar-like features for a given size of the image and another to find tha value of the Haar-like features for a given region of an integral image.